Npc Problems: Vertex Coloring

Details
- Release date: November 18, 2019
- Genre: Casual, Indie, Puzzle
- Developer: Fractal Projects
- Publisher: Fractal Projects
- Metacritic: tbd tbd
- ESRB Rating: Everyone
- Platforms: Steam
Current prices
|
|
Steam
Digital |
$0.99
|
Price history
| All time low | |
| $0.49 | (-51%) |
Description
About the Game
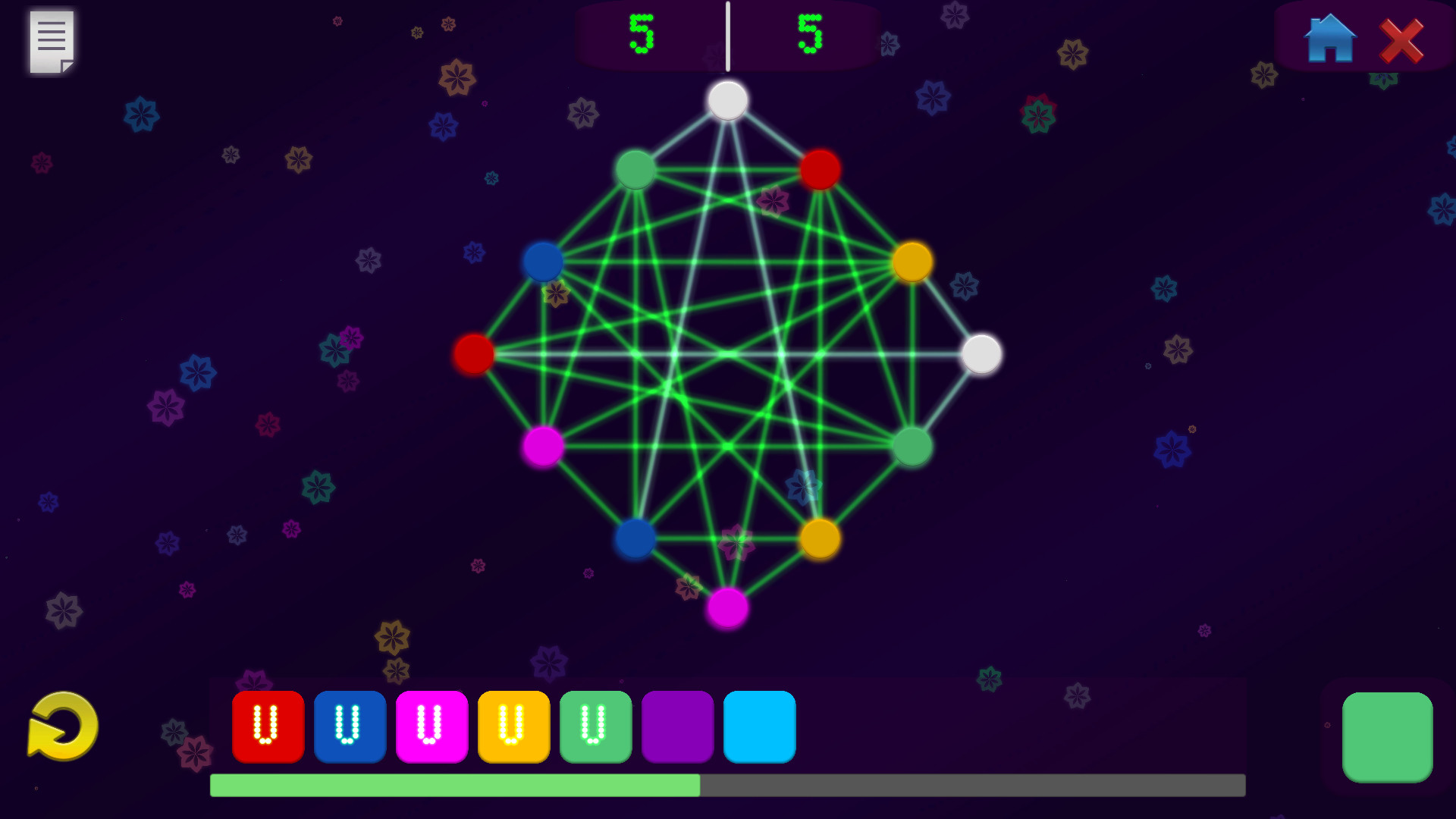
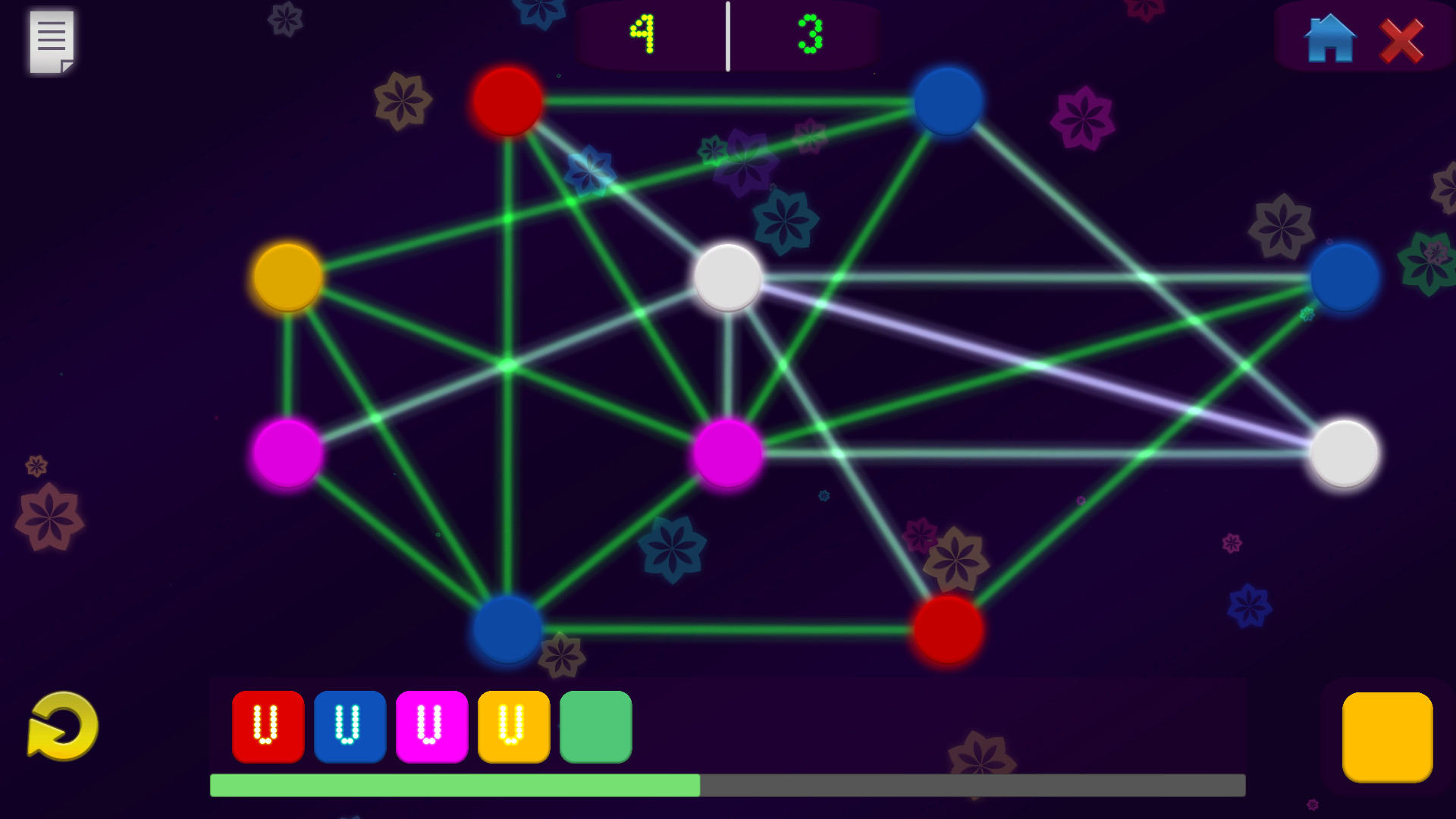
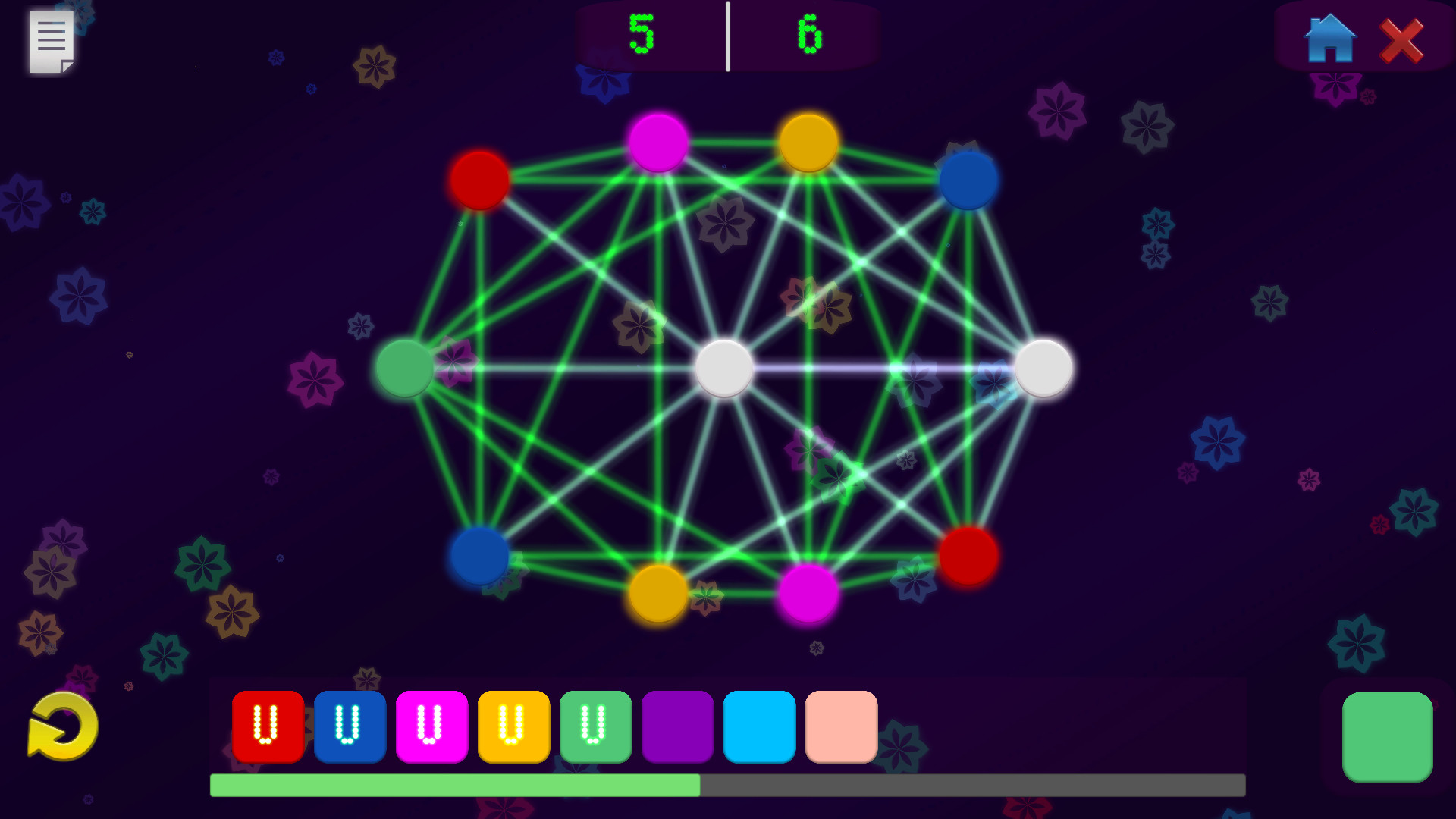
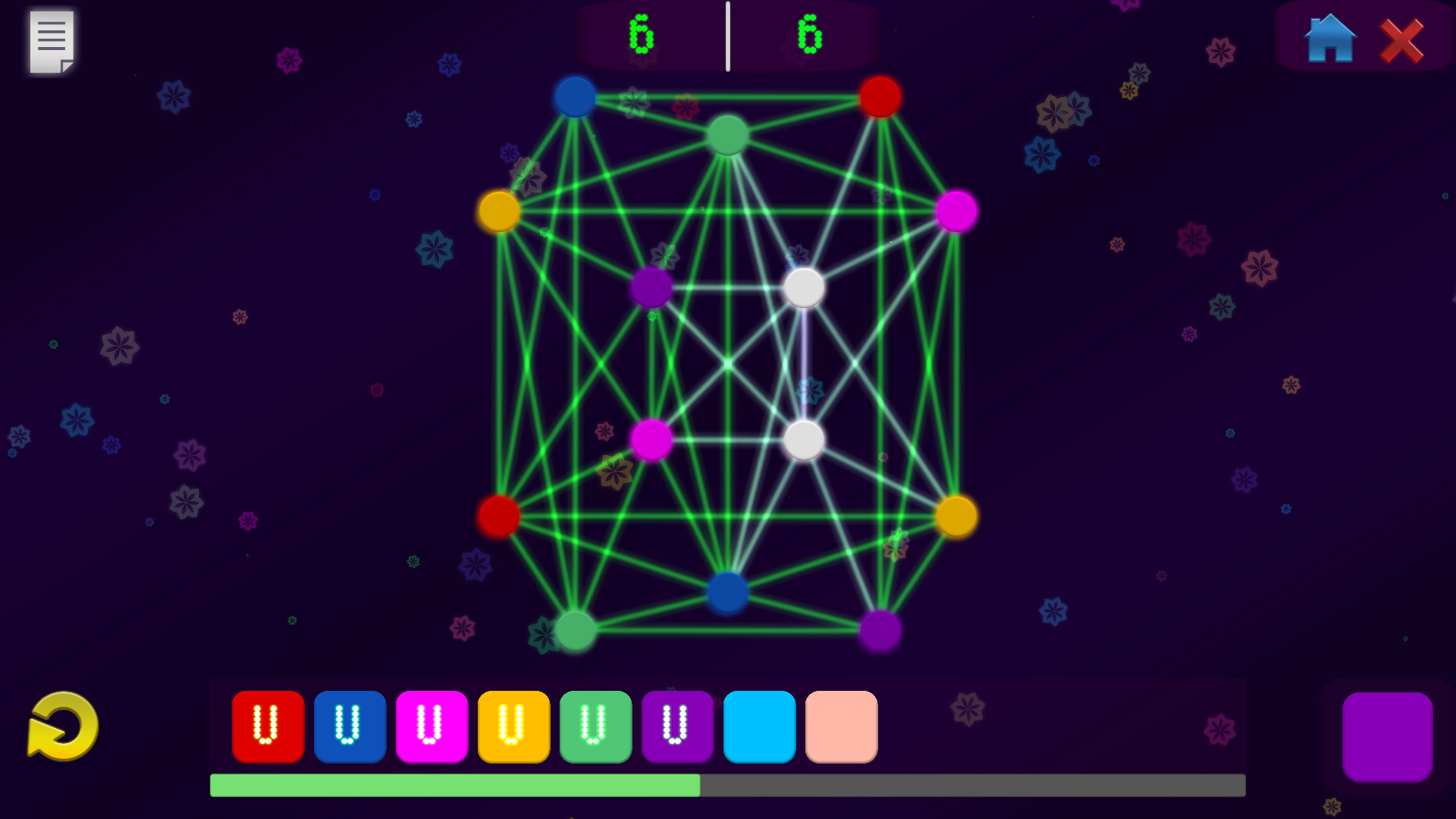
Npc Problems: Vertex Coloring is a minimalistic puzzle game about a real computacional problem.
- An unconventional puzzle game.
- A problem that only artifical intelligence can solve.
- Solve handcrafted instances of the Npc problem vertex coloring.
- Enjoy a relaxing environment with neon graphics and original synthwave musics.
Linked circles cannot have the same color, can you paint all the circles using the minimal number of colors?
Additional information:
The vertex coloring problem is represented by a graph, which is a set of nodes and lines. The lines connect the vertices and are called edges.
The vertex coloring problem is one of the complete non-polynomial (NP-complete) problems. These problems cant be solved by today's computers, they could spend several years to get the solution, depending on the size of the instance. To be able to solve large instances, the using of machine learning and artificial intelligence is necessary. In this game, small relative instances are presented for the player to solve.
There are many real world applications of the vertex coloring problem:
1) Making Schedule or Time Table: Suppose we want to make am exam schedule for a university. We have list different subjects and students enrolled in every subject. Many subjects would have common students (of same batch, some backlog students, etc). How do we schedule the exam so that no two exams with a common student are scheduled at same time? How many minimum time slots are needed to schedule all exams? This problem can be represented as a graph where every vertex is a subject and an edge between two vertices mean there is a common student. So this is a graph coloring problem where minimum number of time slots is equal to the chromatic number of the graph.
2) Mobile Radio Frequency Assignment: When frequencies are assigned to towers, frequencies assigned to all towers at the same location must be different. How to assign frequencies with this constraint? What is the minimum number of frequencies needed? This problem is also an instance of graph coloring problem where every tower represents a vertex and an edge between two towers represents that they are in range of each other.
3) Sudoku: Sudoku is also a variation of Graph coloring problem where every cell represents a vertex. There is an edge between two vertices if they are in same row or same column or same block.
4) Map Coloring: Geographical maps of countries or states where no two adjacent cities cannot be assigned same color. Four colors are sufficient to color any map.
Source:
Videos